者有话要说： 明天见
☆、190
法国曾经是世界数学
心之一，到现在也是数学
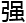国, 只是这些年以来, 以前法国最为骄傲的代数几何随着新一代的年轻数学家崛起, 渐渐的被德国和俄国超过, 尤其是德国的舒尔茨以及布
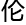德，前后两个超级天才崛起让其他青年数学家黯然失
。
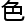法国现在最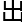
名的代数几何专家是孔涅教授，他的非
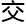换几何十分有名气，现在法国更加侧重于概率论，偏微分方程，尤其是偏微分方程，放
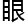全球, 没有一个国家比得上。
洛叶看即将在欧洲数学会上发表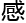
言的数学家, 偏微分方程方面, 
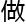一个小时报告的人数最多。
她之前已经见到了舒尔茨，现在又见到了在他之前最为知名的天才西蒙·布德。
早期他的研究重
是微分几何，近两年他的研究成果已经偏向了非线
偏微分方程，他是今年欧洲数学会会奖最力的争夺者, 即将一个小时报告会。
他的报告重就是武义-劳森猜想, 也就是在最小表面理论存在的
期问题，他对这个猜想的证明已经发表在了四大上，这个报告主要是补充和解答。
不得不说，因为主攻方向问题，她对布德并不如对舒尔茨来的关心。
在他的报告第二天要开始的时候洛叶才开始啃他之前发表的论文。
武义-劳森猜想有三十年历史，在三十年间不知
有多少数学家对这个猜想发起了挑战, 最后全都失败，现在由布德解决了这个猜想，而他解决的方法十分人意料，因为他用的方法并不算复杂，甚至可以说十分简单，整个猜想的证明方法也只用了十张纸，可以说让前仆后继对这个猜想发起挑战的数学家崩溃。
——他们准备了这么多的
级武
，居然最后败在了这样一个初级武之
。
心里怎么一个憋屈了得。
而这可以说和洛叶现在
行的工作有异曲同工之妙，洛叶想把超维球
堆积问题的计算方式化繁为简，在看他那短的不行的证明过程时，洛叶似乎有所觉。
洛叶边看边在旁边记录自己的想，不知不觉到了午，洛叶去一楼的餐厅用餐的时候，非常巧就碰到了西蒙·布德，他们居然住在同一家酒店。
洛叶想了想，
脆走上去搭讪，把之前写来的一些问题问当事人好了。
布德看到洛叶只是有些诧异，不过也只是有些，听说她是普林斯顿的学生，跟随教授前来参加欧洲数学会，脸上就不由的
了些许了然。
“……空间和基本群？”
非线偏微分方程，洛叶了解的并不多，洛叶询问的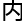
容还是偏向于微分几何，而且洛叶问的还是数学大师约翰·米尔诺在十九世纪发表的一篇论文，表述了空间和基本群的关系。
洛叶，“我注意到你曾经发表的过的论文，Yamabe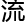
动的收敛，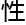
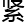凑猜想的反例，里面是有群论相关，负曲率空间的基本群受到曲率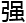烈的约束，必须
备某些特殊的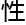质，而基本群也算是拓扑几何的概念。”
数学主要分支有一百多个，可是这些分支之间的联系十分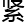密，洛叶研究的群论可以和目前国际
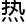门数学研究领域全都挂上勾。
布德，“普利斯曼定理看过吗，它比较详细的表述了曲率如何影响基本群。”
而在旁人看来，两人完全是谈甚
，而在他们旁边的人完全听不懂他们两个在讨论什么。
这个时间正值暑假，来欧洲旅行的不少，比较年轻的像是学生一样的人就忍不住的看向他们两人，有一个还忍不住拍了照片，悄悄的询问同桌，“你们能听得懂他们在什么吗？”
其他人纷纷摇了摇
，“我看报，最近欧洲数学会要在这里召开，他们应该是来参加的人吧。”
“他们看起来一不像是数学家啊。”
“尤其是那个女生，看起来好小。”
在他们印象，数学家应该都是发
白，年过半百，可无论是布德还是洛叶都颠覆了他们的想象，这也太年轻了。
他们是外行，可是餐厅却不乏有行，他们是绝对认得布德的，看着他居然和一个小女生谈甚，他们都不由的想
一睛，确定没有错之后，看洛叶的神就多了几分奇异。
布德也没有想到他居然可以和洛叶基本上没有障碍的去，不但是曲率和基本群，洛叶懂黎曼几何，辛几何，拓扑几何，分形几何，有些涉猎他自己都没有她来的广。
他比洛叶这个学生要忙多了，在不得不结束和她的谈话时，非常诧异的问，“你对几何学的认识明显比代数学要好，为什么要选择的群论？”
洛叶当然不会和他说真的原因，只是，“等我硕博的时候应该会选择代数几何。”
布德，“那应该很快了。”
他20岁就拿到了博士学位，和他比洛叶的度算是慢了，可是经过刚刚的谈，他相信只要他愿意，应该会很快拿到硕士学位和博士学位，他匆匆写了自己的邮箱，“如果你在微分几何上有什么问题可以和我讨论。”
欧洲数学会主要是面向于在欧洲工作以及欧洲籍贯的数学家，布德拿到博士学位后就开始在斯坦福担任教授，现在在哥比亚大学任教，可以说他已经许久没有回过欧洲了，这次回来，不但要准备报告，还要和一众故人联络。
等布德走后，洛叶收好了纸条，吃完剩的东西才继续上楼。
第二天布德的报告会，洛叶也去听了，面的满满的，其不乏知名的数学家。
而布德的补充主要是在对于在他证明武义-劳森猜想运用的的一个泛函方程，正是因为这个泛函方程，让他有了灵光一闪，最终用一个简单无比的方式来证明了这个猜想。
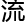而光是一个补充，是无法支撑过一个小时的报告会的，在讲完这个泛函方程后，他又开始讲起了让自己之前发表过微分球面定理（Differential Sphere Theorem），也是对那篇论文一个重要补充，讲其一个关键，三维行几何。
“……任何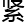致，可定向的三维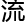行，当用其一些整正互补相互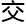的球面和环面去切，对一个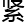致单联通的黎曼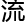行，它的截面曲率位于……”
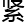“……在截面曲率拼挤条件，常曲率空间形式的致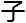
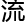行拓扑同胚于球面，当大于四维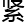，致定向的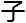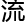行满足于……”
等到布德的报告讲完，面响起了烈的掌声，趁着这掌声洛叶悄然离去。
欧洲数学会的影响力差不多仅次于世界数学会，在这样的会上，
ql请记住本站地址http://m.quanbl.com