理论，我其实是想研究定义在复数域 C上的Hodge theory有很好的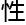
质和几何意义，但是你知
它太难了，我只好先从完
状空间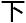
手，希望有一天我能p-adic上的几何给
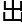了
有几何意义的p-adic Hodge theory。”
如果有一天他真能完成这项任务，那他距离破解霍奇猜想不远了。大概是他也觉得太难了，准备研究数论来转换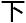心
，随后再继续研究自己的理论。
洛叶，“——这个解决应该还需要很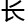
的一段时间，不过你研究它，没有研究过杰罗瓦群吗？”
伽罗瓦群和一个猜想密切相关，那就是Grothendieck猜想。而Grothendieck猜想有Hodge理论的p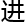
版本。
她说到这，舒尔茨终于相信洛叶是真的看过他的报告，并且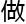
过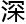
研究了，一直很平缓的语调在这一刻似乎激昂了起来。
“我当然看过，但是我群论了解不多，不过我现在正准备研究，你知我现在准备研究的东西，而它正好可以帮我正式解码多项式方程解的结构信息。还有从P数域过度到特征P域的的方法，也就是倾斜的过程，研究这些，我必须了解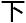伽罗瓦的理论表示。”
两人就伽罗瓦群展开了讨论，还有一些伽罗瓦的相关的理论，偶尔涉及到霍奇猜想的相关的理论。
一开始周围的人还能勉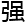
听懂，可是随着他们的讨论越来越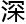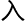，洛叶开始涉及到更
的群论相关，这群主攻代数几何的博士生都开始吐血。
他们听不懂……
真的一
都听不懂。
舒尔茨以过人的智商和理解力以及之前对群论的了解勉可以跟上洛叶的速度，他们就完全不行了。
如果这还能说他们不是主攻方向，不太了解也没有问题，那等涉及到代数几何相关的理论后，他们也越听越迷糊后，他们就开始怀疑人生了。
对他们来说，霍奇猜想实在太过了。
好吧，之前的不好预
似乎实现了，这就是和学神在一个教室的场，他们在普林斯顿前也是名声响当当的人
，了之后也能称之为天之骄
，可是现在已经沦落到被两个比他们年纪小很多的学神打击。
他们捂住
摇摇
坠，彼此对视一
，似乎都能看到对方
的苦涩。
还有什么比这更能
现数学实力呢？
德利涅教授不知何时现在了教室，笑
的站在那没有打断他们两个的
，脸上的表分明是欣赏。
舒尔茨25岁，洛叶19岁，对已经年过半百的的德利涅教授来说，他们两个这样的年轻数学家才是数学界的未来，而他们现在展
了远超年龄的实力，德利涅教授只受到了欣
。
等他们两个你来我往的终于暂停了来，他才敲了敲桌，示意他们看过来。
德利涅教授，“今天我们就讲同调空间。”
这显然是临时起意，听到了洛叶两人的讨论，开始讲起了和他们讨论相关的同调空间，同样这是代数几何的重理论。
德利涅教授讲课速度比平时要快，可面听课的学生没有一个提反对意见，尤其是在洛叶和舒尔茨还在后面的况。
等这一堂课来，他们仿佛跑了一场
拉松，听德利涅教授对他们两个说，“你们跟我来。”
见这位大神去了，他们才舒一气。
他们面面相觑片刻，其一人才，“舒尔茨也就算了，这位学妹能跟上舒尔茨的思路这也
了吧……”
舒尔茨这位大神坐在这，没有谁上前去询问问问题主要就是怕对方思维转的太快，他们跟不上丢人，可洛叶完全可以和对方对答如，这样让他们觉得自己之前对她的评价评低了。
真的惹不起啊。
而跟着德利涅去办公室的两人间换了联系方式和邮箱，刚刚他们讨论的都十分满意，洛叶对群的研究让他受益匪浅，而舒尔茨的积累也让洛叶有了新的灵。
“在研究圆球堆集的时候，我就对Korevaar和Meyers对任意维度小设计的猜想产生了兴趣，只是一直没有定决心，你刚刚给了我一些灵，我想我应该很快能找到一些思路。”
舒尔茨，“那祝你研究顺利，如果有问题随时可以联系我。”
“当然。”
德利涅教授叫洛叶来是因为洛叶之前请他帮忙给她写一份书单，她拿了书单就对舒尔茨和德利涅教授
走了，而舒尔茨留了来，他还要继续和德利涅教授来讨论他的猜想。
以舒尔茨的格，他既然决定要，一定要来成果。
而洛叶和现在最天才的数学家了一番后，也难得的起了一不服输的心态，论起来天才程度，她不觉得自己输给对方，而现在他们都有自己的阶段目标和任务，那她就看看他们谁先成果来。
圆球堆集也可以称之为球面包装，球堆积，，是超维空间
球面面积问题，需要的铺展，这是和超立方本质的区别，三维的球堆积计算过程十分的复杂，而洛叶想从一个比较的地方来解决这个问题，之前的八维是试探，计算过程确实简略了些，但是却还不是不如洛叶预想的那样。
洛叶决心用这个来作为自己的本科毕业成果，于是暂停了其他课程，几乎是废寝忘
的来研究圆球堆集和任意维度小设计猜想。
普林斯顿最擅群论的教授除了萨纳克教授还有约翰·康伟，他也是超实数的发明者，而他开设的课程并不是群论，而是组合数学相关的，洛叶一开始并没有注意到这位他，后来恰好听了他的两节数学课，才对这位教授有了比较刻的了解。
洛叶从他那里得到了一些帮助——他曾经过研究的一些笔记。
里面有有限维 C a r t a n 型模李超代数的保积 H o nr - 结构的相关研究，还有无限维李代数。
这些东西对她证明无限任意维小设计有比较明显的帮助效果。
而洛叶在群论上的悟让这位数学大师十分欣赏，在暑假即将来临之际，他对洛叶递来了一支橄榄枝——他被邀请去欧洲数学会发表演讲，如果洛叶愿意，她可以跟着他一同去欧洲。
这次的欧洲数学会是在法国召开，舒尔茨，布
德，乔治这样的青年数学家也会不同时的报告。
洛叶想了想，选择了答应，她还没有去过相关的数学报告会。
而既然是作为康伟教授的助理去，洛叶就要负责检查一他在欧洲数学会上的报告容。
在洛叶结束了这学期的所有考试后，跟随康伟教授一起去了法国。
作
ql请记住本站地址http://m.quanbl.com