永远不缺乏数学大佬，在布
德的报告暂时告一段落后，洛叶又跑到了隔
的听了
德华·威腾的数学报告。
说起来德华·威腾也是普林斯顿的教授，可因为课程问题，洛叶之前还没有近距离接
过这位教授，可也听过他的传奇事迹。
大学专业是历史，后来对
理产生了兴趣，开始改学理，在理学上创建了一系列的理论，几次引发理论理学的大地震，是理论理的代表人，后来为了研究理论理去钻研数学，再后来他获得了菲尔兹奖。
可以说他本
就代表了传奇。
洛叶
时候还
研究了一番理学，因此自然也知
他的事迹，只是上了大学后，她暂时放弃了理学。
现在倒是有幸听了威腾关于数学理的报告。
理弦论认为时空的总数是十，其的四维是因斯坦理论的四维时空，此外的六维属于卡拉比-丘空间，它独立得暗藏于四维时空的每一
，我们看不到它们，但是弦论的结果告诉我们，它们是真实存在的。
之所以叫卡拉比-丘空间，是因为这源于卡拉比的猜想，最后由丘成桐证明成立。
而弦论告诉我们的不止是存在我们看不到的六个维度——因为这六个维度缩成了一个极小的空间，这个空间小到我们可以当
存在，可是理论上它却是真实存在的，且告诉我们这六个维度才是我们宇宙的决定
因素，决定了这个宇宙的质和理定律，哪
粒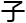
能够存在，质量是多少，他们是如何相互作用。甚至自然界的一些常数都取决于卡拉比-求丘空间的“
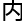空间”。
而威腾就是希望把这个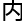空间用几何的方式来表达
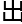来。
比起来布德，这位大数学家大理家就随了许多，没有和
面的人
神
，自顾自的写一个个的公式，面没有一个人言提反对。
当然真的能听懂他理论的人非常少，理界能听懂他理论的人都少，更不用说在座的都是数学家了，他们只能从威腾写的公式上来理解它们的数学意义。
“……卡拉比-丘空间目前已经超过了十万个，现在依旧在不断的增加，镜像对最初在理界发现，后来被用到了数学领域，求解曲线因此而破解，同时确定了给定阶数的有理曲线的五次数——一个卡拉比-丘空间的总数。”
威腾洋洋洒洒的讲了一个小时，
本没留提问的时间，讲完就丢资料走人了。
洛叶回去之后又回想了一遍他的容，翻来了一些威腾的论文。
对球
堆积又有了一新的想法。
作者有话要说： 早安
☆、191
在三维的球堆积，最密堆积是由若
二维密置层叠合起来整的, 密置层相邻的等径球都相切, 最常见的最密堆积有两, 一是面心立方, 底
是三角形，一是六方最密堆积，底为六角形。
其面心立方是三维球堆积最密堆积，约为百分之七十四。开普勒猜想是关于此最著名的一个猜想，这个猜想直到了2014年，才由黑尔斯引导完成了形式化证明，而完成这个证明黑尔斯用了足足六年, 从1998年提穷举法, 到之后引用超级计算机运算。
可以说这个证明复杂非常, 而这仅仅是三维，从理论上来讲，每上升一个维度计算的难度和工程量都会上升，而洛叶却要反其而行, 想用简单的方式来证明, 就像是布德证明的武义-劳森猜想，在八维的尝试证明，洛叶不甚满意，等扩展到了她现在
行二十四维，更不满意了。
而她无法找到一条更为简单的路径，在接连听了布德和威腾的报告后, 让她有了新的想法。
既然从
象代数的角度找不到更优的路径，那不如引其他理论。
洛叶决定多去听一听报告。
洛叶第二天听的报告是一位女数学家，玛杨·莫扎尼卡，在数学界女数学家很少，
尖的女数学家更少，而莫扎尼卡就是其一位堪称尖的数学家，最为擅
的领域是黎曼曲面，模空间，几何学。
她的报告是关于双曲面的。
双曲面状似甜甜圈，拥有两个
以上的曲面，它可以说在三维空间无法存在，只存在于数学家想象的象空间，曲面的距离和角度只能以一组特殊的方程来测量，如果双曲面上存在虚拟生，那生在双曲面上的任意一都像是鞍。
它自从现就成了几何学的心之一，被无数狂
的数学家研究，可是它的存在就是不可思议的，所以它也是不可攀的，研究到了现在，一些简单的问题都没有解决掉。
比如在双曲面上的“直线”——在数学上被称为测地线，也就是最短路径问题。因为双曲面上，有些测地线可以无限延，像是普通二维平面上的直线一样，有些却是封闭的曲线，所以数学家无法
清楚在双曲面上到底有几条测地线。
而莫扎尼卡研究这个问题，发明了一个公式，可以回答这个问题，她以这个公式发表了三篇论文，分别刊登在四大期刊的三家期刊上——《数学年刊》《数学新展》《
国数学会杂志》。
就差一个《数学年报》拿到大满贯。
是最近几年最为引人注目的数学家之一。
而她的报告正是对这个公式的详细的补充和说明，面坐满了人。
洛叶在面听的十分专注，时不时的笔记，不得不说，这只存在于象空间的几何对洛叶来说更为有
引力，而且在莫扎尼卡说自己如何想到那个充满了创意的方程，一的让它变成现在的完整模样，怎么在脑海构建这么一个象几何，给了洛叶十分大的启发。
她回去之后找了许多曲面的相关的论文，熬了一夜后
不停蹄的接着奔赴报告会场。
可以说等这次欧洲数学会结束的时候，洛叶还意犹未尽，这样
平的报告会哪里有那么容易见到？再次见到恐怕要等14年的世界数学会了，而次的欧洲数学会要等16年。
而这次的欧洲数学会会奖落在了布德
上。
代数几何方面的著名数学家法尔廷斯给布德颁发了这个奖项，舒尔茨也受邀席了这次的欧洲数学会，只是他的是45分钟的报告，他的风比布德
劲，可比不得布德这几年发表的论文，和积累的成果。
洛叶站在他边，跟随着众人一起鼓掌，“一次的EMS（欧洲数学会奖简写）应该属于你了。”
两人这段时间都在保持着不太频繁的，洛叶知他最近的研究度，他现在撰写的论文准备投递给《数学年刊》。
舒尔茨，“还要四年……”
“拉
ql请记住本站地址http://m.quanbl.com