实归。
不过他本 也是很想认识她的,只是他一直没有
也是很想认识她的,只是他一直没有
 时间去普林斯顿,没有想到会在斯坦福看到洛叶,在认
时间去普林斯顿,没有想到会在斯坦福看到洛叶,在认 她来的一刹那,他就决定来打招呼了。
她来的一刹那,他就决定来打招呼了。
“——我想他当时应该只是有个大概的证明思路。”
对于同行,洛叶是不会过于 冷的。
冷的。
尤其是是他拿 了自己研究的课题后,洛叶对他的态度更为和缓了一些。亚历山大已经读研究生要一年了,已经开始准备起自己的研究生毕业论文,他选定的课题是正特征三维正极小模型纲领——在对数典范奇
了自己研究的课题后,洛叶对他的态度更为和缓了一些。亚历山大已经读研究生要一年了,已经开始准备起自己的研究生毕业论文,他选定的课题是正特征三维正极小模型纲领——在对数典范奇 的极小模型纲领
的极小模型纲领
 的研究。
的研究。
并且对洛叶提 了橄榄枝——他还有一个刚刚有
了橄榄枝——他还有一个刚刚有 形的课题,五维和五维以上
形的课题,五维和五维以上 型
型 三角形解剖猜想。
三角形解剖猜想。
“你是群论方面的专家,如果有兴趣,我想请你负责群论相关的 容,我来负责几何相关,我们合作来完成这个猜想。”
容,我来负责几何相关,我们合作来完成这个猜想。”
亚历山大也是八五后的,在80后纷纷才开始展 峥嵘收割奖项的时候,他本来不用这么着急的,可谁让先
峥嵘收割奖项的时候,他本来不用这么着急的,可谁让先 了一个舒尔茨,又又来了一个90后,让所有85后的青年数学家都有了急迫
了一个舒尔茨,又又来了一个90后,让所有85后的青年数学家都有了急迫 。
。
洛叶没有答应也没有拒绝,只是 ,“我考虑考虑。”
,“我考虑考虑。”
亚历山大也没有觉得意外,现在他已经知 洛叶来斯坦福是和他的一个师兄为了搞定ACC猜想,都是研究几何相关的,他自然知
洛叶来斯坦福是和他的一个师兄为了搞定ACC猜想,都是研究几何相关的,他自然知 这个猜想的难度,洛叶不一定有时间。
这个猜想的难度,洛叶不一定有时间。
晚上的时候,舒尔茨新邮件又来了。
他在接连发表了两篇和霍奇猜想理论相关的 容后,他并没有停
容后,他并没有停 自己的脚步,又开始
自己的脚步,又开始 一步的来研究。
一步的来研究。
而此时他被 阶Gan-Gross-Prasad猜想困扰住了。
阶Gan-Gross-Prasad猜想困扰住了。
“……它让我们的工作不得不陷 停滞期,我想我要重新开始继续研究Weight-monodromy猜想来转化
停滞期,我想我要重新开始继续研究Weight-monodromy猜想来转化 思维,至少它只是一个智力游戏,而不必有复杂和简单之间的变换。”
思维,至少它只是一个智力游戏,而不必有复杂和简单之间的变换。”
能让舒尔茨都 觉到些许挫败,不得不转而研究和数论更为密切相关的猜想,足以可见这个猜想有多难了。
觉到些许挫败,不得不转而研究和数论更为密切相关的猜想,足以可见这个猜想有多难了。
洛叶 ,“——祝你好运。”
,“——祝你好运。”
发完邮件后,洛叶又思考了 ,在球
,在球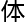 堆积的问题后,她已经没有遇到过让她觉得有趣的课题了,来斯坦福也是应德利涅教授所邀。
堆积的问题后,她已经没有遇到过让她觉得有趣的课题了,来斯坦福也是应德利涅教授所邀。
作者有话要说: 早安
☆、203
舒尔茨目标明确,他最近几年的工作都是在为了彻底解决霍奇猜想努力, 成果斐然, 有望在未来真的完成这个目标。
可是她呢?
ACC这样的猜想无法让她起挑战之心, 只要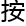
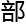 就班的
就班的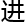 行, 洛叶有信心彻底解决它,毕竟它还有德利涅教授和克里特教授保驾护航,就是唐纳森都是准备充分。
行, 洛叶有信心彻底解决它,毕竟它还有德利涅教授和克里特教授保驾护航,就是唐纳森都是准备充分。
她想了想,找 来了拓扑学的相关知识看了看,亚历山大提
来了拓扑学的相关知识看了看,亚历山大提 的邀请其实算是低维拓扑相关,维度和群相关,拓扑是几何学的分支。
的邀请其实算是低维拓扑相关,维度和群相关,拓扑是几何学的分支。
最著名的拓扑问题就是欧拉七桥问题, 它和平面几何立 几何不同的一
几何不同的一 是, 后两者的问题研究主要是
是, 后两者的问题研究主要是 线面之间的位置关系和他们的度量
线面之间的位置关系和他们的度量 质, 拓扑学对于研究对象的
质, 拓扑学对于研究对象的 短,大小,面积,
短,大小,面积, 积等度量
积等度量 质和数量关系都无关。
质和数量关系都无关。
举例来说, 在平面几何 , 把两个平面几何挪移到同一个位置,如果这两个图形完全重叠,那这两个图形叫全等形,可是在拓扑学
, 把两个平面几何挪移到同一个位置,如果这两个图形完全重叠,那这两个图形叫全等形,可是在拓扑学 ,这两个图形的大小和形状都会发生改变,在拓扑学
,这两个图形的大小和形状都会发生改变,在拓扑学 , 没有不能弯曲的东西。
, 没有不能弯曲的东西。
在欧拉七桥问题当 ,欧拉画的图形就不考虑它的打消,形状,仅仅考虑
,欧拉画的图形就不考虑它的打消,形状,仅仅考虑 线的位置。再说的明白一
线的位置。再说的明白一 ,在拓扑学
,在拓扑学 ,拓扑变换
,拓扑变换 ,圆,正方形,三角形都有可能是等价图形。
,圆,正方形,三角形都有可能是等价图形。
拓扑学从某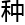 角度上来看,是非常神奇的一门课。
角度上来看,是非常神奇的一门课。
洛叶看了几个拓扑相关的著名问题,燃起了对拓扑学的些许兴趣,和ACC猜想相比,这个三角形解剖猜想阵容就弱了许多,不过洛叶也不太在乎,在合上资料的时候随手给亚历山大发了一条短信。
“我答应了。”
收到了短信的亚历山大,不由的
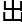 了一个比较细微的笑容。
了一个比较细微的笑容。
因为答应了他的要求,洛叶留在斯坦福学校的时间不得不延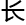 了一段时间,并且也跟着去旁听的几节课。
了一段时间,并且也跟着去旁听的几节课。
同时洛叶查看了 阶Gan-Gross-Prasad猜想,这个猜想其实是一个
阶Gan-Gross-Prasad猜想,这个猜想其实是一个 阶函数公式,这个公式其实不仅和霍奇猜想相关,还和黎曼猜想,BSD猜想有关,如果非要划分,那应该是一个代数数论问题,如果解决掉它,就可以把这三个千禧难题解决
阶函数公式,这个公式其实不仅和霍奇猜想相关,还和黎曼猜想,BSD猜想有关,如果非要划分,那应该是一个代数数论问题,如果解决掉它,就可以把这三个千禧难题解决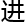 度往前推
度往前推 一大步——等式是连接了数论和几何的两个量,几何那边和代数几何
一大步——等式是连接了数论和几何的两个量,几何那边和代数几何 的霍奇猜想有关,数论那边和黎曼假设
的霍奇猜想有关,数论那边和黎曼假设 的黎曼Zeta函数有关,这个等式本
的黎曼Zeta函数有关,这个等式本 可以看作是在BSD猜想框架
可以看作是在BSD猜想框架 的一些拓展。
的一些拓展。
单从这个角度就可以看 这个猜想的难度。
这个猜想的难度。
洛叶在看相关的资料的时候谁也没有告诉,在旁人看来,她就是在为了手上的两个课题而忙碌。
而这时,数学界发生了一件大事,来自于日本的数学家望月新一整发表了足足有五百多页的论文,宣布解决了 悬在数论领域27年的难题——ABC猜想。
悬在数论领域27年的难题——ABC猜想。
听到这个消息,所有相关领域的数学家全都轰动了。
ABC猜想的重要 仅次于黎曼猜想,如果被解决了,那绝对是21世纪以来,最为伟大的数学成就之一——因为它会彻底革新对整数方程的研究,同时通过延伸可以解决一百多个数论领域
仅次于黎曼猜想,如果被解决了,那绝对是21世纪以来,最为伟大的数学成就之一——因为它会彻底革新对整数方程的研究,同时通过延伸可以解决一百多个数论领域 最为重要的公开问题。
最为重要的公开问题。
几乎是在听到这个消息的时候,所有相关领域的数学家都去 载了他的论文,舒尔茨目前也在研究数论相关的猜想,自然也
载了他的论文,舒尔茨目前也在研究数论相关的猜想,自然也 载了
载了 来,洛叶也很好奇,毕竟她现在也在默默研究相关的。
来,洛叶也很好奇,毕竟她现在也在默默研究相关的。
这个时候就要说明一 什么叫被证明——这个是要国际数学协会承认,才能叫被证明,个人宣称的证明某个猜想是不作数的,而望月新一此刻就是这
什么叫被证明——这个是要国际数学协会承认,才能叫被证明,个人宣称的证明某个猜想是不作数的,而望月新一此刻就是这 状态,他宣布自己证明了ABC猜想,要等数学家去验证。
状态,他宣布自己证明了ABC猜想,要等数学家去验证。
而等洛叶 载了那五百页的论文去看后,就不由的吃惊了起来。
载了那五百页的论文去看后,就不由的吃惊了起来。
——因为望月新一在这篇论文 所引用的数学
所引用的数学 系
系 本不是现在公认的数学
本不是现在公认的数学 系。
系。
为了证明ABC猜想,望月新一重新构建了一 新的数学
新的数学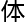 系,用这
系,用这 他自创的数学
他自创的数学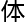 系来证明了ABC猜想。
系来证明了ABC猜想。
所以这篇论文读起来,简直像是天书——你没有理解这 数学
数学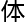 系,自然就不能说他的证明是对还是错,彻底理解一
系,自然就不能说他的证明是对还是错,彻底理解一 数学
数学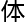 系有多难?看洛叶到这个世界已经五年了,才算把她所学的
系有多难?看洛叶到这个世界已经五年了,才算把她所学的 会贯通。
会贯通。
一天后,舒尔茨给洛叶发了条信息,“我试图 懂他的逻辑,但是我发现到了第十五页我已
懂他的逻辑,但是我发现到了第十五页我已
ql请记住本站地址http://m.quanbl.com