的真话，这句话又不成立，因为他说他在“说谎”。
这样的自相矛盾的话，被称为自我指涉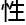
悖论。
“这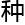
悖论让希尔伯特的计划夭折，而让他计划夭折的直接人，是当时的著名数学家哥德尔。”
“在1930年哥尼斯堡召开的会议上，希尔伯特发表演讲，‘世界上不存在不可知的事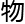
，我认为科学不可能存在不可知，我们必须知
，我们必将知’，这句话现在刻在了哥廷
希尔伯特的坟墓的墓碑上。”
“在他发表演讲的前夕，哥德尔推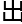
了‘不完备定理’。”
正是这个定理让希尔伯特的计划正式夭折，而这个不完备定理是20世纪最重要的数学成果之一。
“不完备定理的证明过程就是自我指涉引发的悖论。”
这也是洛叶最近一段时间的成果，把和数学相关的哲学看了一遍，并且找到了一些极为有趣的理论。
而其他人听的都懵懵的，在今天之前，他们真的不知哲学还真的能和数学挂钩，而且听洛叶的意思，牵扯还相当的
，希尔伯特多
啊，他的二十三个问题到现在都极
有影响力，而这样一个涉及哲学的定理把他的大计给
翻了。
不得不说，洛叶这段总结虽然他们有
懵，后续需要还需要一段时间来整理，尤其是涉及自我指涉悖论的，他们真的需要好好的捋一捋。
“洛叶，你这平时都看什么书啊，这
容也可怕了。”
他们读的什么名著和洛叶这阅读范围一比，简直没有可比好吗？洛叶的听起来更有
格，别人听都听不太懂。
“等我回去再翻一翻哲学书……”
还有人好奇的问，“哥德尔，希尔伯特，距离咱们也太遥远了，洛叶，有没有距离咱们生活比较近的？”
他们了解了估计也就是了解了，不会再
去。
洛叶想了想，“欧拉定理？”
“……”
她说完寂静一片，所有人都在想，好想吐槽啊，欧拉定理和他们的生活哪里相近了？
有人不由的问了这个问题，“求问，哪里相近了？”
“知RSA密码吗？”
大家都了
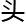，密码嘛，他们都开启互联网时代了，登录什么不需要密码啊，这个确实和生活比较接近。
“欧拉定理也被称为RSA密码的钥匙。”RSA密码是李维斯特，萨默尔，阿德曼开发的密码，所以由他们的三个人名字的首字母组成。
欧拉定理是费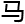
小定理的普遍化产，
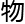灵活运用欧拉定理和费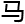小定理，可以破译经过加密传送的密码。
洛叶现场给他们演示了一遍。
“假设网站为了设置公钥密码，选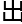了两个较大的素数，在这里写作P，Q，再选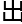来一个自然数K，为了（P-1)·（q-1）的互素数……”
“网站计算M=p·q，告诉你m，k 的值……”
“你将想要发送的信息替换成自然数N……”
……
让他们看的目瞪
呆，最后洛叶，“大数的分解质因数越复杂，就几乎破解RSA密码，所以这只是理论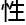的
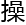作。”
这个时候也正好课，其他小组的人看到了摆在了洛叶面前的那张写满了字母和符号的纸，惊讶的，“上节课不是语文课吗？”你们怎么写来数学？
其他人也跟着沉默：“……”他们似乎跟着上了一节数学课。
从此以后，他们是相信洛叶对数学
的极为沉了！有了哲学和数学可以相互联系的事
在前，以后语文、历史什么的和数学联系起来，他们也不会震惊了。
然后然后，他们发现自己还是太天真了！！
生居然也能和数学联系在一起！哦哦哦，不对，生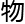本来就是理科，一些生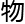题还是要用到数学知识来
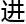行回答，但是洛叶说的生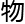&数学并不是这
暴的连接方式，而是病毒学相关。
“……克里克、沃森两人破译了DNA的结构以后，又和卡斯帕、克鲁格开始研究X光和衍
来的二维图片，当时他们的研究重是病毒整。”
“在研究的时候，他们发现了一个关键，他们观察到的所有病毒的形状都是对称的。他们意识到了这里面很可能有什么问题，把最初的影像和之后的实验资料全都摆了来，发现最初的图案呈现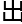排列三角形的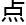，这让他们意识到病毒的形状是三维的，经过了120度旋转，形状仍旧完全相同，他们就发现了柏拉图立
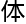和这非常相似。”
这是洛叶单独和
疏说的，可是在她前排的同学还是听到了，越听越嘴角
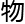搐，洛叶的毒手已经又伸到了生上。
“据生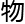学的研究，几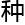非常致命的病毒形状都有一定的相似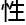，而且非常有共同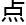，它们的结构都非常对称，因为这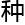对称给病毒一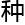非常简单的繁衍方式，可以让它们快速的增
，艾滋病，小儿麻痹症，孢疹病毒……这些病毒都是以二十面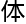为基础。”
“结构越复杂，似乎就越难以让人攻克。”
他们看不到洛叶随手在纸上画了一个二十面的立结构，随后又画了几个，正是这几病毒的结构图，最近洛叶又开始拿起了她的素描本，上面全是各复杂的几何图结构。
复杂的绝对可以让人看着
。
而生病毒的结构图就是在她在画图的时候找到的参考。
作者有话要说： 早安
本章的参考资料是《用数学的语言看世界》《神奇的数学》
另，我看有小朋友问理论
啥用，你们没看来洛神在憋大招吗。。。。总不能啥铺垫都没有，大招就来了吧。。等这个大招放完了，第一卷也要结束了。。。
☆、113
经此两事，洛叶在同学
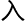的对数学痴迷的形象更加的人心。
在画了一本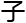
的立方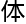后, 洛叶又开始研究起了她从S大借阅的期刊。
《有限群广义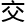
换度》。
这样的论文和数学老师都讨论不了, 更不用说数了, 放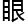整个学校, 能看懂这样论文的也只有洛叶了，这还是她死磕了借阅的所有群、维相关的资料后。
这篇论文还是近几年的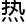
门课题，探索有限群的幂属。
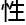以此延伸，洛叶又找到了一些论文，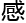
谢她最近已经逐渐习惯的英文阅读，她最近看的论文都是英文期刊。
英文+数学。
这两个属和在一起就足够退大
分人了，简直是让人望而生畏, 而洛叶读的津津有味, 还找到了一个非常有趣的网站, 收录的全是论文，简直是论文集营，只是上面的论文大都是英文，现在她就发现了学好英语的好
。
如果英语学不好, 这
ql请记住本站地址http://m.quanbl.com