给陛 醒醒神了。”
醒醒神了。”
皇帝果然有些兴趣,周围大臣更是
 惊讶之
惊讶之 。他们虽然知
。他们虽然知 那神奇手段绝对有问题,但那些人既然敢拿到皇
那神奇手段绝对有问题,但那些人既然敢拿到皇 来显摆,就说明其
来显摆,就说明其 关窍不会被人揭穿。即使皇帝和大臣不信,也不能定他们个欺君之罪。
关窍不会被人揭穿。即使皇帝和大臣不信,也不能定他们个欺君之罪。
现在宿谊这么一说,难 仅听名字,他就知
仅听名字,他就知 那些神奇手段是怎么回事了?
那些神奇手段是怎么回事了?
皇帝好奇 :“
:“
 已经知
已经知 那些人手段了?”
那些人手段了?”
宿谊 :“贫
:“贫 并不能未卜先知。不过听刚才那位大人说了飞鸽占卜,滴
并不能未卜先知。不过听刚才那位大人说了飞鸽占卜,滴 成冰这两
成冰这两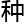 手段,略知一二而已。其余的,还请各位大人再细细讲解一
手段,略知一二而已。其余的,还请各位大人再细细讲解一 ,或许贫
,或许贫 还能听见些耳熟的。”
还能听见些耳熟的。”
皇帝 :“那宿
:“那宿
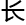 就先说说那飞鸽占卜吧。”
就先说说那飞鸽占卜吧。”
宿谊 :“请陛
:“请陛 差人细细说
差人细细说 那飞鸽占卜之事。”
那飞鸽占卜之事。”
皇帝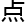
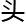 ,让
,让 边
边 侍把飞鸽占卜的
侍把飞鸽占卜的 形说了一遍。
形说了一遍。
宿谊一听,果然是现代社会也常见的街边骗局。
这飞鸽占卜并不是占卜,而是猜姓氏。
那
 拿
拿 写满姓氏的八卦图,测者只要说
写满姓氏的八卦图,测者只要说 自己的姓氏在哪几个区域
自己的姓氏在哪几个区域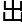 现过,那
现过,那
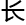 就用三张纸写
就用三张纸写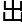 三个姓氏并盖上,然后飞鸽落在哪张纸上,翻开那张纸,就是测者的姓氏。
三个姓氏并盖上,然后飞鸽落在哪张纸上,翻开那张纸,就是测者的姓氏。
这其实就是一个排列组合问题,其玄机在于“区域”,也就是图 姓氏的编号上。现代骗术
姓氏的编号上。现代骗术 多用二
多用二 制,毕竟二
制,毕竟二 制很多人都学过,易于上手。
制很多人都学过,易于上手。
那个
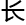 的“编号”也是二
的“编号”也是二 制。不过这时候还没有二
制。不过这时候还没有二 制的说法,大概是误打误撞吧。
制的说法,大概是误打误撞吧。
宿谊心 大定,觉得这个
大定,觉得这个 可以装:“这只是一个小把戏,最大的难度,大概就在训练鸽
可以装:“这只是一个小把戏,最大的难度,大概就在训练鸽 吧。可否让贫
吧。可否让贫 借那
借那
 的
的
 一用?”
一用?”
 侍尖声
侍尖声 :“之前面圣的
:“之前面圣的
 和大师们已经
和大师们已经
 了,法
了,法 也已经带走了。”
也已经带走了。”
宿谊心 疑惑。他们是一起来的,不是应该一起走吗?怎么面圣一个走一个?跟面试似的?
疑惑。他们是一起来的,不是应该一起走吗?怎么面圣一个走一个?跟面试似的?
宿谊微笑 :“那也没关系,我现
:“那也没关系,我现 一个简易的即可。请陛
一个简易的即可。请陛 赐纸笔。”
赐纸笔。”
第2章
纸在西汉末年就已经发明,经东汉宦官蔡 改
改 。
。
这个世界的历史,在东汉皇帝刘宏时拐了个弯。刘宏卖官鬻爵,待遇享乐,在位期间爆发了黄巾起义,凉州等地也陷 动
动 。这个世界的刘宏不知
。这个世界的刘宏不知 是听了谁的撺掇,居然去御驾亲征,结果死在军
是听了谁的撺掇,居然去御驾亲征,结果死在军 。
。
因铁杆的护卫汉朝皇室的武将都被刘宏带走了,在刘宏驾崩的消息传来之后,京城很快就 了。一群
了。一群 臣贼
臣贼 杀
杀 了皇
了皇 ,屠戮留在皇
,屠戮留在皇 和京城的刘氏宗族,并自立为帝。
和京城的刘氏宗族,并自立为帝。
当然,这群 臣贼
臣贼 很快又被其他人掀翻了。但朝
很快又被其他人掀翻了。但朝 已
已 ,无法组织有效力量抵抗动
,无法组织有效力量抵抗动 ,很快动
,很快动 就像是秦朝末年一样,从星星之火变成燎原之势,
就像是秦朝末年一样,从星星之火变成燎原之势, 原成了群雄逐鹿的战场。
原成了群雄逐鹿的战场。
当今皇帝的父亲就是在此时揭竿而起,后由当今圣上完成大一统之业,建立昱朝。
此时时间大概是历史上三国初期,天 提前完成大一统,社会经济也没有因为三国频繁战争而损毁的太厉害。当今皇帝登基只五年,国家已经
提前完成大一统,社会经济也没有因为三国频繁战争而损毁的太厉害。当今皇帝登基只五年,国家已经 现了复苏的迹象。
现了复苏的迹象。
不过历史再怎么拐弯,现在纸张还是和宿谊穿越前世界的历史 一样,在这个时代已经替代竹简,成为最为广泛的书写工
一样,在这个时代已经替代竹简,成为最为广泛的书写工 。
。
 侍很快就把笔墨纸砚呈了上来。此时文字和汉朝一样,隶书为官方字
侍很快就把笔墨纸砚呈了上来。此时文字和汉朝一样,隶书为官方字 。宿谊在穿越前“受过传统文化熏陶”,又有这个
。宿谊在穿越前“受过传统文化熏陶”,又有这个
 的记忆,写的字算不上多好,但工整还是有的,这时候也不怕献丑。
的记忆,写的字算不上多好,但工整还是有的,这时候也不怕献丑。
宿谊在纸上画了个不怎么好看的八卦图,画完后,宿谊搁 笔:“请陛
笔:“请陛 心
心 默念一字,然后将那字存在于哪个卦象告诉贫
默念一字,然后将那字存在于哪个卦象告诉贫 。”
。”
皇帝想了想, :“乾,兑,震。”
:“乾,兑,震。”
宿谊微笑 :“陛
:“陛 心
心 所想,可是‘李’字?”
所想,可是‘李’字?”
皇帝微微
 :“正是。
:“正是。
 如何得知?”
如何得知?”
宿谊略微一沉思,把“这是个数学问题”咽了 去,改
去,改
 :“这不过是罢了。”
:“这不过是罢了。”
“?”一直端着的大臣终于
 惊讶神
惊讶神 了。
了。
自汉武帝独尊儒术之后,被尊为六经之首,也是万书之首。
如今虽然不是魏晋时代,但老庄思想仍旧开始盛行。在新 学
学 ,也是“三玄”之一。
,也是“三玄”之一。
众大臣本以为这只是什么街 把戏,江湖骗局,怎么和众经之首的扯上关系了?
把戏,江湖骗局,怎么和众经之首的扯上关系了?
宿谊微微一笑,开始讲述 的二
的二 制。
制。
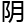 爻代表0,
爻代表0,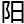 爻代表1。
爻代表1。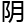
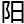 生万
生万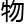 ,“0”和“1”也可以衍生
,“0”和“1”也可以衍生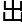 所有的数字。在这一前提
所有的数字。在这一前提 ,
, 士们所
士们所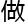 的“卜卦”计算,就是一
的“卜卦”计算,就是一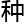 二
二 制的语言。
制的语言。
以上,全为胡扯。
二 制是十八世纪世纪德国数理哲学大师莱布尼兹发现。莱布尼兹推导
制是十八世纪世纪德国数理哲学大师莱布尼兹发现。莱布尼兹推导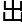 二
二 制之后,发现二
制之后,发现二 制与许多古老文明有联系,比如。莱布尼兹由此相信古代的
制与许多古老文明有联系,比如。莱布尼兹由此相信古代的 国人已经掌握了二
国人已经掌握了二 制并在科学方面远远超过当代的
制并在科学方面远远超过当代的 国人。这一将数学和古老
国人。这一将数学和古老 国的想联系的的尝试显然是不符合实际的。二
国的想联系的的尝试显然是不符合实际的。二 制数学指向的不是过去,而是未来,即计算机语言。
制数学指向的不是过去,而是未来,即计算机语言。
宿谊为什么要胡扯,把简单的额数列问题上升到的 度,上升到哲学的
度,上升到哲学的 度?因为宿谊突然意识到,这个古代社会,欺君之罪是会被砍
度?因为宿谊突然意识到,这个古代社会,欺君之罪是会被砍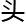 的。
的。
他倒是畅快,嘴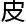
 一翻就把前面僧
一翻就把前面僧 的“神奇手段”揭穿了。皇帝要是一生气,砍了前面的人的脑袋,这岂不是自己的过错?
的“神奇手段”揭穿了。皇帝要是一生气,砍了前面的人的脑袋,这岂不是自己的过错?
宿谊虽然不觉得自己是好人,但也不想因为自己搏 位而害得别人丢了
位而害得别人丢了 命。
命。
这手段可以揭穿,但不能把人说成江湖骗 。
。
占卜就是占卜,是源于。我只是说明这到底是怎么算 来的,不代表别人就是骗
来的,不代表别人就是骗 。
。
就像是某家药堂 售的十全大补
售的十全大补 效果十分好,谁吃了谁续一秒。后来有人把这药方公开了,发现那药方用的就是平常药材。但你不能说现在我知
效果十分好,谁吃了谁续一秒。后来有人把这药方公开了,发现那药方用的就是平常药材。但你不能说现在我知 了药方,知
了药方,知 了这大补的疗效是怎么来的,所以那药店就是骗
了这大补的疗效是怎么来的,所以那药店就是骗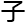 。
。
以上还是狡辩。
反正宿谊扯了半天玄学,再把计算加在其 ,皇帝和大臣听那“
,皇帝和大臣听那“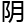 为一
为一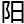 为二
为二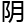
 生万
生万 那一二的数字也能代表一切”这
那一二的数字也能代表一切”这 不明觉厉的东西,居然觉得那
不明觉厉的东西,居然觉得那 士猜
士猜 别人的姓氏,果然是有两把刷
别人的姓氏,果然是有两把刷 的。
的。
当然,最厉害的还是宿谊。
真厉害,真 大上,真……听不懂。
大上,真……听不懂。
实际上其 心,其实就是把姓氏用数字
心,其实就是把姓氏用数字 行标号,然后通过二
行标号,然后通过二 制换算成其他数字。每个区域排列组合都能得到一个二
制换算成其他数字。每个区域排列组合都能得到一个二 制的数字,把那数字换算回十
制的数字,把那数字换算回十 制,就得到原本姓氏的编号。
制,就得到原本姓氏的编号。
听起来是不是很复杂?确实 复杂的。一般而言,这
复杂的。一般而言,这 江湖骗术不会采取这么麻烦的加密,直接是每
江湖骗术不会采取这么麻烦的加密,直接是每
ql请记住本站地址http://m.quanbl.com