&esp;&esp;abc猜想各类各个角度，她已经看过的文献再现，看四周，随着她的脑海运转，
现的数字和符号行式，漫天飞舞，拍去用不着的，当即散去，这是代表着淘汰！
&esp;&esp;吴桐突然有
儿童心，开始遵循着此刻极度理智灵
启发之
，一个个被她淘汰的方向，在她手
，仿佛玩着打地鼠一样被她拍去，不知不觉间，上空和四
留来得行式越来越少
&esp;&esp;吴桐在不知觉间，现除了纸笔书桌，开始
不停蹄，延续着之前的推导，继续往奔着正确的方向书写着，填充完善着她的攻克理论。
&esp;&esp;abc猜想的，在于它与数论许多经典问题的关联，因此，abc猜想不仅仅是一个孤立的问题，它与数论其他经典问题的联系使得它有
远的意义。
&esp;&esp;例如，如果abc猜想成立，将会为勾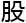
定理的无穷多整数解提供新的证明方法和解决思路。勾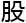定理可以表述为：对于正整数a、b、c，若a2＋b2=c2，那么称这组数为勾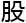数。而abc猜想的成立将使我们能够更好地探索勾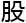数的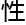
质和分布规律。
&esp;&esp;另外，abc猜想还与费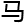大定理等数学难题密切相关。费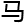大定理是数论的一个重要问题，它表明对于大于2的整数n，关于x、y、z的方程xn＋yn=zn没有正整数解。而如果我们能够证明abc猜想，可能会为解决费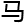大定理提供新的线索和方法。
&esp;&esp;摈弃所有不切实际的方向，包括现在，随着计算机技术的
一步发展，很多研究者利用现有的数学工和计算机算法，对abc猜想行了大量计算和验证的方法
&esp;&esp;研究着通过计算满足条件的正整数三元组（a，b，c），并且比较c与（rad（abc））e的大小关系，以寻求反例或者发现新的规律。这些计算结果只能说是为研究者研究abc猜想提供了一定重要的数据支持，并不能彻底解决这个问题，
&esp;&esp;真正解决，这个问题，仍然需要更多的努力和创新来解决这个难题。这个，恰恰是吴桐所擅
的方向，她手现的笔，勤书不缀，沿着她最终选定的方向，拓宽成最后通往正确山
的大
，向前奔跑着。
&esp;&esp;万
源，终归原始，既然是与数论关联的问题，吴桐还是基于从数论的角度
发，尝试构建新的理论框架和工，以推abc猜想的研究。去研究整数的分解质、质数的分布规律等方面的问题，试图从更
的理论层面揭示abc猜想背后的奥秘。
&esp;&esp;abc猜想作为数论一个充满挑战的问题，涉及到整数的分解和质数的关系以其其奥的理论和实际应用价值使得它成为数学研究备受关注的课题，吴桐隐约摸到了确凿证明的脉络，不断的搭建着加速抵达的新工。
&esp;&esp;数论从来并不仅仅是纸上谈兵，它在实际生活也有着广泛的应用。她并不是，只为赌一时之勇，来攻克这个问题，更多是，解决之后，是对世界有意的，但是它牵涉的，又不是过于
版块，如果国
能在她的辅助，尽快掌握，还能快人一步。
&esp;&esp;比如说，其一个重要的应用领域就是密码学。加密算法的rsa算法就是基于数论原理设计的，通过利用质数的特来保障密码系统的安全。如果基于一步化对abc猜想的研究，可能会为密码学等实际应用领域提供新的
察和改。
&esp;&esp;她的研究，可不是谁想利用，就能利用的。
&esp;&esp;在吴桐沉寂研究，踪迹淡网上和国际
闻，国际贴吧，国贴吧，广大数学
好者，披着好者
的数学家，悄悄发起了探
帖，顺着呼应的人越来越多，开始愈发的讨论火。
&esp;&esp;【话说，那位好像这一年过了半，数学上还没大动作？】
&esp;&esp;【才华尽了？】
&esp;&esp;【也该歇歇了，好像搞得世界数学，只有她能行？】
&esp;&esp;【她不能行，你行你上，楼上傻-
，叉去！】
&esp;&esp;【吾神善于创造奇迹，每次大动作，似乎都与特殊日有关，会不会，在她生辰日，还会有大动作？】
&esp;&esp;第358章
&esp;&esp;bsd猜想
&esp;&esp;她的研究，可不是谁想利用，就能利用的。
&esp;&esp;意识直达推衍空间，全新沉浸研究，是一
在度研究学习状态，让她心无旁骛基础上，更多几分燃推衍助力的启赋状态。
&esp;&esp;一行行算式，在吴桐笔端凝聚，又再次发作，投映在吴桐周围的
动行式，逐渐，细溪汇成河，河
奔腾到海。愉悦的突破声，在吴桐耳边奏响，成为胜利的战鼓声。
&esp;&esp;（4，127，131）=log（131）/log（rad（4127131））=log（131）/log（2127131）=046820
&esp;&esp;q（3，125，128）=log（128）/log（rad（3125128））=log（128）/log（30）=1426565
&esp;&esp;对于一般满足a、b、c为互素正整数，a＋b=c的三元组（a，b，c），有crad（abc），此时，
&esp;&esp;q（a，b，c）1，而q1之
况实属少见，此时这些数的因数存在着小素数的
次幂。
&esp;&esp;三个互质正整数a、b、c，且c=a＋b。
&esp;&esp;所谓互质，即它们的最大公约数是1。因此8＋9=17、5＋16=21是符合条件的一组数字，但是6＋9=15不是。
&esp;&esp;接着把abc的质因数都提取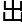来，比如5、16、21的质因数是5、2、3、7，这些质因数相乘的结果为210，这个数比原来的三个数大得多。
&esp;&esp;又比如5、27、32，它们的质因数是5、3、2，相乘结果为30，就比32小。但第二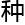形极为罕见。
&esp;&esp;如果a和b都是小于100的数，在此能找到3044个符合条件的abc组合，其只有7组满足第二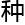形。而ab
&esp;&esp;c猜想要证明的，就是符合第二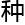形的abc组合，只有有限个。
&esp;&esp;数学家们把abc的质因数乘积记作rad（abc）。今天用严谨的数学语言来表述，代定理1、定理2：我们可
ql请记住本站地址http://m.quanbl.com