&esp;&esp;第一站,吴桐去了成老办公室。
&esp;&esp;“老师!”吴桐探 ,见老师没在忙着,才推门而
,见老师没在忙着,才推门而 。
。
&esp;&esp;“回来了?怎么不休息休息?”成华南笑着起 ,打量了
,打量了 吴桐的气
吴桐的气 ,不错,没在西洲受委屈,也没被风沙
,不错,没在西洲受委屈,也没被风沙 着。
着。
&esp;&esp;pl-15研发制备成功,超优 能,因着他是吴桐的老师,又参与过弹
能,因着他是吴桐的老师,又参与过弹 新材料研究,他在知
新材料研究,他在知 人范围,这样的突破
人范围,这样的突破 成果,让他狠狠在
成果,让他狠狠在 层小众圈
层小众圈 里被人艳羡了一把。有个开山大徒弟专
里被人艳羡了一把。有个开山大徒弟专 于前,现在幼徒也异军突起,立足
于前,现在幼徒也异军突起,立足 尖,他这辈
尖,他这辈 ,太值了!
,太值了!
&esp;&esp;“给您当面拜个晚到的年!”吴桐笑着在老师的招呼 就坐。“这一周基本都在调整休息,回到学校,静极思动,就来您这里走走,给您捎带
就坐。“这一周基本都在调整休息,回到学校,静极思动,就来您这里走走,给您捎带 儿西洲特产,华总给准备的,我借
儿西洲特产,华总给准备的,我借 献佛!”
献佛!”
&esp;&esp;和老师说说话,聊聊近况,吴桐就告辞离开材料学院, 一步,去了数院。年前她的那一堆事,都是数院师
一步,去了数院。年前她的那一堆事,都是数院师 帮忙
帮忙 持,她回到学校,于
持,她回到学校,于 于理,也得去找师
于理,也得去找师 报备一声。
报备一声。
&esp;&esp;“可算是回来了,一切都顺利吧!”潘文华看到吴桐,不由笑逐颜开,哎唷,他们这日盼夜盼,总算把吴桐给盼回来。
&esp;&esp;就怕吴桐这一去,没有时日,要是项目有些耽搁,卡上两三年都是常事。虽然,吴桐一向以 效
效 了名,这一次,事涉绝密,他们也没消息渠
了名,这一次,事涉绝密,他们也没消息渠 ,没有
,没有
 信息来源,就有些忐忑。他赶
信息来源,就有些忐忑。他赶 让人去请周文平和李轶生过来。
让人去请周文平和李轶生过来。
&esp;&esp;就在楼上楼 办公室,被请的两人到来很快。
办公室,被请的两人到来很快。
&esp;&esp;“顺利的,潘院,好久不见,周老师,李老师!”吴桐笑着问候:“为你们 一声,迟到的新年好!”
一声,迟到的新年好!”
&esp;&esp;“新年好,新年好,吴桐!”见到你就是新年正月最好的福气,两位老师展颜愉悦笑意满满溢 。
。
&esp;&esp;潘文华从展示柜 ,取
,取 珍重放在特制匣
珍重放在特制匣 里保存的三枚奖牌三份证书,递到吴桐面前:“你的奖牌证书,都在我这里保存,总算能够
里保存的三枚奖牌三份证书,递到吴桐面前:“你的奖牌证书,都在我这里保存,总算能够 归原主,奖金也都打到你的账上了!”
归原主,奖金也都打到你的账上了!”
&esp;&esp;“谢谢潘院,谢谢周老师,李老师,又你们费心了!”吴桐很惭愧,她把事 一丢,让师
一丢,让师 费心费力,自己一去几个月,没有音讯。
费心费力,自己一去几个月,没有音讯。
&esp;&esp;“这么光荣的事,我们费 儿心思都心甘
儿心思都心甘 愿,这次回来还走吗?”潘院不便打探吴桐执行的什么任务,只关心吴桐
愿,这次回来还走吗?”潘院不便打探吴桐执行的什么任务,只关心吴桐 面是否还要继续。
面是否还要继续。
&esp;&esp;吴桐摇 。“不了,已经完结了。接
。“不了,已经完结了。接 来,我要全心放在数学上一段时间,最近不会再碰材料,先把我的数学课题
来,我要全心放在数学上一段时间,最近不会再碰材料,先把我的数学课题 好!”她这个数学系的学生,名不副实,从
好!”她这个数学系的学生,名不副实,从 学以来,一直都在材料学,动力、工程各方面打转,反倒是本职专业,摆
学以来,一直都在材料学,动力、工程各方面打转,反倒是本职专业,摆 的时间最少。
的时间最少。
&esp;&esp;吴桐决定,最近收心回到最纯粹的数学之上,好好把自己的数学课题专研透,在毕业前,
 些亮
些亮 的成果,
的成果, 化她的数学储备,也让师
化她的数学储备,也让师 更有荣光。
更有荣光。
&esp;&esp;“以后,我可要常来数院转悠,老师们可别嫌烦!”
&esp;&esp;“不会,不会,我们 迎着呢!”吴桐重归专心研究数学,这是个再好不过的消息,潘院几人觉得,这是他们今年开年后听到的最动听消息!
迎着呢!”吴桐重归专心研究数学,这是个再好不过的消息,潘院几人觉得,这是他们今年开年后听到的最动听消息!
&esp;&esp;“数研 心的办公室永远为你敞开着,随时
心的办公室永远为你敞开着,随时 迎你过去!”周文平赶
迎你过去!”周文平赶 邀请,让吴桐多去数研
邀请,让吴桐多去数研 心转转,这可是他们数研
心转转,这可是他们数研 心崭新的牌面。
心崭新的牌面。
&esp;&esp;“好的,回 我天天去报到,天天在您面前晃悠,晃悠到周老师该嫌我烦了!”吴桐逗趣。
我天天去报到,天天在您面前晃悠,晃悠到周老师该嫌我烦了!”吴桐逗趣。
&esp;&esp;顿时间,办公室 笑作一片,但是三位师
笑作一片,但是三位师 心里,却是统一,吴桐就是时时刻刻在他们
心里,却是统一,吴桐就是时时刻刻在他们
 底
底 转悠,也没人会嫌她烦的。
转悠,也没人会嫌她烦的。
&esp;&esp;第198章
&esp;&esp;循环
&esp;&esp;吴桐向来言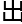 必行,说是回归数学界,就立即行动。哥德
必行,说是回归数学界,就立即行动。哥德 赫猜想这个课题,已经拖了太久,零零碎碎的钻研,太过片段,到底不如全
赫猜想这个课题,已经拖了太久,零零碎碎的钻研,太过片段,到底不如全 心的投
心的投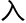 。
。
&esp;&esp;她开始固定往数研 心、图书馆,宿舍三
心、图书馆,宿舍三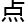 一线,全
一线,全 心投
心投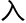 对哥德
对哥德 赫猜想的攻关之
赫猜想的攻关之 ,前人的手稿,被她反复研读,筛法,圆法,各
,前人的手稿,被她反复研读,筛法,圆法,各 被人尝试用来攻克哥德
被人尝试用来攻克哥德 赫猜想的法门,吴桐都有尝试过,她需要一个来攻克哥德
赫猜想的法门,吴桐都有尝试过,她需要一个来攻克哥德 赫猜想的工
赫猜想的工 。
。
&esp;&esp;都说筛法走到了尽 ,在亲自上手后,吴桐并不认同这个观
,在亲自上手后,吴桐并不认同这个观 ,她最终确认。还是要再筛法上
,她最终确认。还是要再筛法上
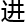 步,奠基成攀爬哥猜巅峰的
步,奠基成攀爬哥猜巅峰的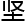 实阶梯。
实阶梯。
&esp;&esp;吴桐想要尽快把哥猜所涉及的资料研究完毕,顺利的话,三月里完成这个课题,之后可能有时间回家待一段时间,接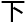 来等待一到两个月的毕业答辩,准备毕业就可。
来等待一到两个月的毕业答辩,准备毕业就可。
&esp;&esp;想到能回家待上一到两个月,吴桐的 劲儿就更足了。凡是题目,必有答案。用心钻研,吴桐快乐而沉浸,困扰世人裹足不前的难
劲儿就更足了。凡是题目,必有答案。用心钻研,吴桐快乐而沉浸,困扰世人裹足不前的难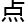 儿,对她来说,只是难上一些的台阶,不是不可逾越。
儿,对她来说,只是难上一些的台阶,不是不可逾越。
&esp;&esp;吴桐最终选择圆法引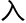 筛法,对筛法
筛法,对筛法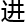 行补充创新。
行补充创新。
&esp;&esp;在研究诸多数论问题时,往往都会用到母函数(neratgfunction)。比如在研究素数分布时我们会用到dirichlet级数通过 用perron公式,f(s)的解析
用perron公式,f(s)的解析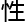 质便能用来研究诸多积
质便能用来研究诸多积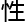 数论问题
数论问题
&esp;&esp;通过对圆法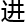 行更加巧妙地运用,已经有先人证明了,几乎所有偶数都满足
行更加巧妙地运用,已经有先人证明了,几乎所有偶数都满足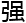 哥德
哥德 赫猜想
赫猜想
&esp;&esp;筛法其实是一个更加广的思想。利用这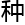 方法,可以对一些数论量
方法,可以对一些数论量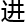 行估计。举个最简单的例
行估计。举个最简单的例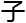 ,如果用π(x,z)表示大小不超过x但所有素因
,如果用π(x,z)表示大小不超过x但所有素因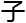 都大于z的正整数个数:
都大于z的正整数个数:
&esp;&esp;π(x,z)就是一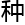 典型的筛函数。筛法便是用来估计这类函数的方法。筛法在哥德
典型的筛函数。筛法便是用来估计这类函数的方法。筛法在哥德 赫问题
赫问题 扮演着重要角
扮演着重要角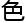 、确切地说,{a,b}问题的研究
、确切地说,{a,b}问题的研究 采用的是这
采用的是这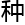 形式的筛法
形式的筛法
&esp;&esp;吴桐思考着筛法和圆法,一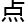 儿一
儿一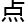 儿的推导,怎么样能把它们巧妙地结合,铸就攻克哥猜的登天之梯。
儿的推导,怎么样能把它们巧妙地结合,铸就攻克哥猜的登天之梯。
&esp;&esp;n=p1+p2+p3(素数p1,p2,p3均≥3)的解数
&esp;&esp;a+b的问题,归 结底还是一
结底还是一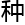 对哥德
对哥德 赫才想的复杂表述,每个大偶数n都可以表述为a+b其
赫才想的复杂表述,每个大偶数n都可以表述为a+b其 ab的素数因
ab的素数因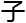 因
因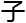 个数,分别不超过a和b,,当a=b=1的时候,问题自然而然再次回归最初的表达,任一大于2的偶数,都可写成两个素数之和。
个数,分别不超过a和b,,当a=b=1的时候,问题自然而然再次回归最初的表达,任一大于2的偶数,都可写成两个素数之和。
&esp
ql请记住本站地址http://m.quanbl.com